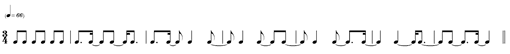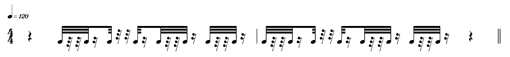Purloined Rhythms
Consider the following:
| (ex. 1) |  |
As things go, this pattern is not overly complex.
The same pattern, with a dot added to each note:
| (ex. 2) |  |
This adds a small amount of complexity, given that we may tend to count (ex. 2) in terms of
| (ex. 3) |  |
as opposed to thinking 1 or 2 
notes throughout, as in
| (ex. 4) |  |
Note that this problem of how to group data is hardly unique to music.1
Now consider the following apparently arbitrary syncopated interruptions.
(ex. 5)
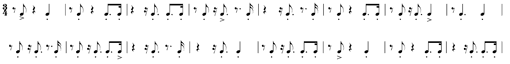
(Click on image for enlarged version)
What (if any) is the relation between this and (ex. 1) or (ex. 2) above?
Counting the number of 
notes from attack to attack, one finds exactly the pattern of (ex. 2) above, except that the pattern is written with short notes and rests. The pattern repeats every 9 attacks (the start of the repeat is indicated by an >), and the first 4 loops are present in their entirety, plus the first 8 attacks of the next loop.2
Why is the identical ratio of attacks so much harder to recognize when written as in (ex. 5), as opposed to (ex. 1) or (ex. 2)?
At least three reasons come to mind:
- Ex. 5 consists of short notes with rests in-between the attacks. In (ex. 5), not only do we have many more note-symbols to process than in (ex. 1) or (ex. 2), but we may process these additional note-symbols from each note-symbol to the next, thereby hindering our ability to perceive and group the larger functional units.
- Ex. 5 does not start on the downbeat. Given our predilection to view THINGS in terms of the bar-line and the meter, THINGS which possess their own shape or pattern (whether that be rhythmic, motivic, or harmonic) may — especially if they "loop" — appear to be syncopated, or re-stressed, or may even appear to have NO pattern at all; this even though the THING itself is NOT internally syncopated and does NOT lack for pattern. In other words, the THING itself does not change. It is we who insist upon using the nominal meter as a distortive lens.
- Ex. 5 is 39 long, and as such, rarely aligns with the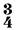
meter (which = 36 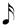). Even if the pattern originally started on a downbeat (and (ex. 5) does not), each time the pattern repeats, it "moves over" by three 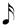, thereby guaranteeing an appearance ever-changing from the original presentation. This can be seen in (ex. 6)
Footnotes
- For example, consider the following taxi-cab license plate:
T426426T.
Do you first see these numbers — think of them — remember them — as:
42
64
26
or
426
426 - In the actual composition, one finds, simultaneous with other material, both (ex. 1) and (ex. 2) in rhythmic canon. When performing this, one must be certain to preserve, across both rates of speed, the pattern's rhythmic trajectory. The accentuation within the pattern must NOT be switched — just as one should NOT switch the trajectory or accentuation of a pitch canon.
which superimposes the loops of (ex. 5) one on top of the other, the only restriction being that the initial attacks are vertically aligned.3
In short, because of the rhythmic notation forced upon us by the Time Signature (hereinafter TS), a rhythmic pattern whose components or sum are not evenly divisible by or within the TS in which the pattern occurs, almost always assumes an appearance that is, at best, misleading.4
Frequently, a rhythm may appear complex because the composer is using constant values in a context which does not easily allow for that; and such simple patterns or constant values may suffer the most from the vagaries imposed by the TS.
Consider (ex. 7):
(Click on image for enlarged version)
Each of these 12 attacks are a 
, or 3 
or 6 apart, but because these equidistant attacks are superimposed upon a background of changing TSs, it is difficult to perceive the uniform duration between attacks.
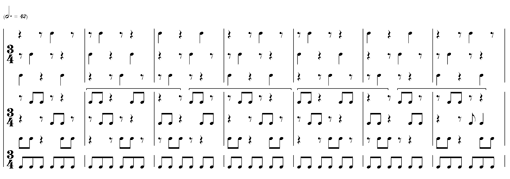
The following is another example of equidistant attacks. Here, because of "when" the succession starts, the unfortunate, put-upon composer is forced into an astonishingly piss-poor alternative equal 
notation.
(ex. 8)
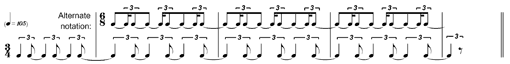
(Click on image for enlarged version)
In (ex. 9), the notation conspires against our realization that the double bass has 4 groups of attacks, each group containing 6 equal-valued notes, the trajectory of each group of 6 being identical to the previous, except at a slower pace.
(ex. 9)
(Click on image for enlarged version)
- Not only is the rhythmic notation different for each of the first 4 loops, but because of that notational difference, the horizontal space each loop inhabits may also vary in an individual part (note that that may not be the case in the score, especially if there are running
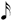). Therefore, equal horizontal page-space does not mean equal time, and because of that, the rate at which the eye scans the page may change; and that change cannot but add to the problem of perceiving, understanding and recognizing the identity of the rhythmic patterns.
- Inevitably, there will be "those" who will invariably raise the argument that what is needed is to convey both the pattern, and its placement relative to the TS grid. Not only can that not be done (as I have repeatedly argued elsewhere) but, in the case of the composer of (ex. 5), he has made it crystal clear in his didactic writings that such was NOT his intent, the bar-line being only a notational convenience, or more likely a convention; and that caveat is true for at least every composer cited within this text. Furthermore, and in my opinion, this is the dispositive argument — our present system of rhythmic notation does not allow, or only allows under extreme duress, the simple notation of patterns which are not aliquant with the nominal meter; hence, one should give the "benefit of the doubt" to, or acknowledge the existence of, patterns which do not conform to the nominal meter, as it is an absurdity to posit that, just because it is not specifically allowed, it is therefore enjoined!
Further generalizable examples follow.5
Ex. 10 is a 
, plain and simple.
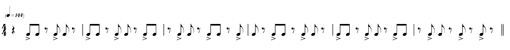
(Click on image for enlarged version)
Here, from a not very similar composer, is a similar grouping by 3.
(ex. 11)
(Click on image for enlarged version)
- As a class assignment, students should be asked to find (on their own) examples similar to those given. Once aware of the existence of such situations, and given the special spectacles needed to see them, the students, with a little cleverness, will find that the fields are rife!
Speaking of grouping by 3, here is a group of people all of whom are in 3, but at different rates.6
(ex.12)
(Click on image for enlarged version)
- When performing this, the performer(s) should concentrate on the "three-ness" of the individual part(s), and the accuracy of the duration from the start of each group of three to the next start, while remaining aware of the difference between rates; this is more important than worrying excessively about the precise synchrony with the beat, or exact relations to the other parts.
Rather than think of (ex. 12) as repetitions of 3 things (i.e. two notes plus a rest), it may prove simplest to think only of the attacks, which simplification is presented in (ex. 13).7
Ex. 14 is a 
.
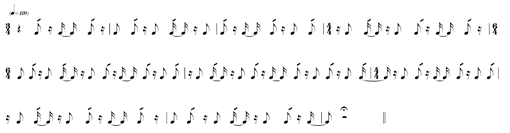
(Click on image for enlarged version)
Even though this repetitive pattern could hardly be called complex, note the need (because of the TS/bar-line diktat) to notate the same 2-attack pattern in three different ways.
| (ex. 15) |  |
Ex. 16 is in 
(see the brackets which delineate the 4+5). If one ignores the first 2 notes of the top voice, it a 3 part (rhythmic) canon.
(ex. 16)
(Click on image for enlarged version)
In the complete score, the is not only highlighted by the 3 parts at the top of the score, but the conflicts with the lowest voice, which is beamed sometimes by 3, and other times by 2.
(ex. 17)
(Click on image for enlarged version)
Of course you may give yourself a hernia syncopating the following -- it is a free country!
(ex. 18)
(Click on image for enlarged version)
For those not wishing to patronize the medical profession, it will be simpler to think of the above as a pattern where the upper voice (the triangle part) expands (n + 1), each note being longer by 1 up to a value of 16 ,
(ex. 19)
(Click on image for enlarged version)
- This type of organization is easily traced back to the composer's 1962 work for 100 mechanical metronomes.
while the lower (bass drum) voice, starting from 16 , contracts at the rate of one per note.8
Here is a permutation cycle, or if you prefer, a rotating pattern (in the right hand: abcd/abdc/acbd/acdb etc; the left hand starts: bacd/badc etc) where:
| (ex. 20) |  |
(ex. 21)
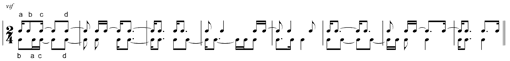
(Click on image for enlarged version)
This example allows for a discussion of some MOST crucial aspects.
- Given that every 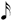is present in the surrounding texture, it is easy, conceivable, and far more interesting (both for the player and the overall musical "gestalt") to perform the series "per se", as opposed to the syncopations.
First of these is that, whether played by a single pianist (as in this specific work), or distributed between two or more instrumentalists, it is ABSOLUTELY IMPERATIVE that the rhythm resulting from combining the lines (the combination, or sometimes the composite, rhythm) be known, and indeed, be written out.9
In the case of (ex. 21) that combination rhythm results in:
(ex. 22)
Rewritten in this manner one finds another level of pattern rotation, which can be further clarified as follows:
we stated above that, in (ex. 21) 4 elements were being permuted. The sum of these 4 elements = 5 i.e.
| (ex. 23) |  |
Therefore it probably behooves us to think in terms of 
i.e. 4 bars of , rather than the 5 bars of 
of (ex. 22) above.
(ex. 24)
In this fashion the underlying pattern is fused to its fundamental meter, thereby simplifying and allowing the passage to stand (in the complete original) in clear metric contrast to the other instrumentalist in this work (the flute), for whom this process is fairly irrelevant, as that player is in a different metric world.
Lest you think these concerns, manipulations, suggestions and solutions apply only to the music of our recent past, allow me to draw your attention to an example from 1597.
- I believe this to be so important a point that there will eventually be an article devoted just to that activity.
Remember that in those days there was no score, and the parts had no bar-lines. Temporal relations between parts and participants was controlled by an apparently all-so-simple coding, known as mensuration signs. Sadly, this coding is no longer in (common) use, and if we want to perform the work, we must transcribe it into what is today a more recognizable language.10
Here it is in score-form, (ex. 25) in a "modern" edition, where these quoted measures look "tricky", perchance fussy or bustling, even disorient. Something does not "fit".
(ex. 25)
This is how the same measures appear in a modern version much more analogous to the original.
(ex. 26)
(Click on image for enlarged version)
Gone are the struggles to place the dotted rhythms against a grid, which struggles almost forces one to frantically hack at the underlying thrust or trajectory of the phrase.
- Note that the composer of 1597 would probably be just as uncomfortable with, and incomprehending of, today's notation, as we are with his original! Nor can we posit, with any confidence whatsoever, that what is today the norm constitutes, in any overall sense, an improvement over the original. Indeed, today's notation may very well detract at least as much as it solves.
Suddenly the tripping groups of assume their proper visage and flow, and the simultaneous manifold opposing metrical frames appear. Furthermore, the notation instantly clarifies that there is a relationship between the swinging groups of and the subsequent groups of of the following section (not shown here). Unfortunately, for today's performers, as regards the vertical (temporal) alignment of the parts, this version is not as clear as is the previous, and the argument then arises as to which of these two modern versions is practicably preferable, but that (especially as the question is not easily answerable) is fortunately beyond the scope of this present text.11
What is it that we are to take away from all of the above?
The crux is:
in the notation of rhythmic patterns, what you see is not necessarily what you "get" or what it is; and in order to understand and get closer to your rhythmic problems, you may need to rewrite them, to re-express them. At the risk of distressing at least one very close friend, rhythmic problems are (in some ways) similar to algebraic equations or, if you prefer, problems in topology, where shapes which may appear to be different are actually closely related, while other shapes which appear superficially similar are in fact of different classifications. I am not proposing a complete topsyturvyfication of everything you have ever learnt about rhythm, but I am suggesting that you take your rhythmic problems and unfold them. Spread them out. Re-define them. One need not equal Raymond Queneau's 99 retellings of "Exercices de Style",12 or the attempted precision and care of Ponge's "La Table"13 but I know of nothing that will more quickly get you to the rhythmic, and usually the musical, nub of the matter; to the weights, the balancing forces, the rhythmic motivic expansions and contractions, the thrust or trajectory of the phrase, than to try to re-work a rhythm, ESPECIALLY those that you think you understand.
Naming or classifying something can sometimes help us to recognize the thing in question. What might we call rhythmic problems similar to those described above?
Edgar Allen Poe's The Purloined Letter (1844(-1850)) and Arthur Conan Doyle's The Naval Treaty (1894) are two detective stories of how letters purportedly stolen, are actually in place, but hidden in plain sight, and can only be found by people who know how and where to look. In honor of these two tales, let us call these hidden-in-plain-sight-rhythms "purloined" (although that is not the original meaning of the word).
The moral, then, of OUR story is:
LOOK FOR PATTERNS THAT ARE HIDDEN IN PLAIN VIEW.
Look for patterns that may not be/ARE NOT, related to the nominal TS, which is a grid imposed for many different reasons that may or may not be relevant to the patterns in question.
Do not allow yourself to be mentally hog-tied by a blind, brainless and bureaucratic bar-line and TS.
Give life to all non-conforming patterns, so that there exists a vibrant multiplicity and democracy in the rhythmic texture, as opposed to just the imposed (f)rigidity of the time signature!
In short, MARCH TO THE PATTERN'S OWN DRUMMER!
Paul Zukofsky
May 2005
List of Citations
Example 5 — Messiaen, Olivier. Trois Petites Liturgies I (1943) {11 meas. after reh. #6} to {4 meas. before reh #8}: pizz. strings; Durand.
Example 6 — Messiaen, Olivier. Trois Petites Liturgies I (1943) {11 bars after reh. #6} to {4 bars before reh #8}: pizz. strings; Durand.
(Also see Messiaen, Olivier. Technique de mon Langage Musical [The Technique of my Musical Language]. A. Leduc. 1944.
and Messiaen, Olivier. Traité de rythme de couleurs et d'ornithologie en sept tomes [Treatise on rhythm, color, and ornithology] (1949-1992). A. Leduc. 1994.)
Example 7 — Babbitt, Milton. Septet but Equal (1992) {meas. 237-243}: piano; CF Peters Corporation.
Example 8 — Carter, Elliott. String Quartet #3 (1971) {meas. 299-303}: violin; Associated Music Publishers.
Example 9 — Messiaen, Olivier. Turangalila (1947-9) IVth movement {reh. #1} to {7 meas. after reh. #1}: pizz. strings; Durand.
Example 10 — Copland, Aaron. Music for the Theatre (1925) {6 bars before reh. #20} to {reh. #20}: bassoon and tambourine; Boosey & Hawkes.
Example 11 — Schoenberg, Arnold. Variationen für Orchester, op. 31 (1926/8) VIIth Variation {meas. 257-258}: cymbal; Universal Editions.
Example 12 — Ligeti, György. Ramifications (1968-9) {meas. 13-14}: strings; Schott.
Example 13 — after Ligeti, György. Ramifications (1968-9) {meas. 13-14}: strings; Schott.
(Also see Ligeti, György. Poème Symphonique (1962) Schott. 1982.)
Example 14 — Birtwistle, Harrison. Down by the Greenwood Side (1969) {reh. letter Y to reh. letter Z}: Universal Editions.
Example 15 — from Birtwistle, Harrison. Down by the Greenwood Side (1969) {reh. letter Y to reh. letter Z}: Universal Editions.
Example 16 — Schoenberg, Arnold. Suite, op. 29 (1925) IIIrd movement {meas. 167-173}: strings; Philharmonia.
Example 17 — Schoenberg, Arnold. Suite, op. 29 (1925) IIIrd movement {meas. 167-173}: strings, clarinet, and piano; Philharmonia.
Example 18 — Messiaen, Olivier. Turangalila (1947-9) VIIth movement {reh. #7 to reh. #9}: triangle and bass drum; Durand.
Example 21 — Messiaen, Olivier. Le Merle Noir (1951) Vif {meas. 91-5}: piano; Leduc.
Example 25 — Morley, Thomas. A Plaine and Easie Introduction to Practicall Musicke (1597). Ed. Alec R. Harman. J.M. Dent and Sons LTD. 1952.
Example 26 — Morley as transcribed by Charles Wuorinen; from "Notes on the Performance of Contemporary Music." Perspectives of New Music, Vol. 3, No. 1. 1964.
- However, I would be remiss were I not to state that practicality is not everything, and while (ex. 25) may appear easier to perform, if (to paraphrase Stravinsky on tempo) you do not have, or at least understand and know, the intended and natural trajectory of phrase, of what point is the synchrony?
- Paris: Gallimard, 1982.
- Paris: Gallimard, 2002.