|
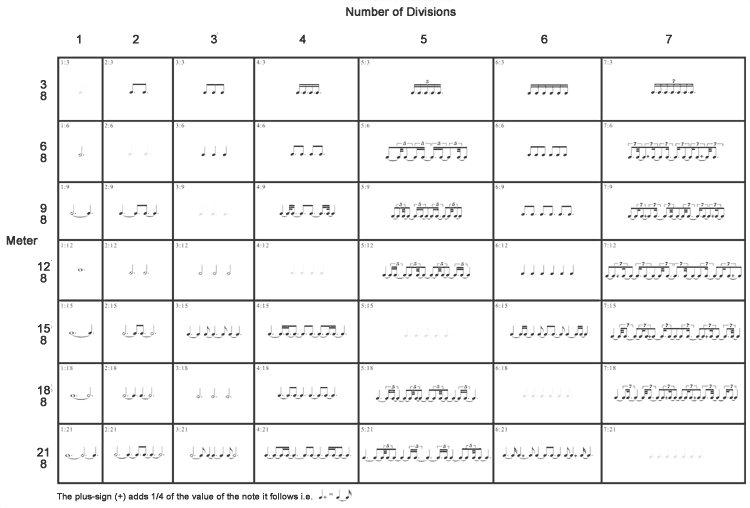
The above matrix (hereinafter EM2) provides patterns for the exact placement for 49 varieties of embedded rhythms. It is similar to Embedded Matrix #1 (hereinafter EM1) except that in this instance, it is the 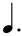 that is the basis for all given meters. The differences between EM1 and EM2 are primarily notational, and everything said in the EM1 explanation still holds; however, the specifics of precisely locating embedded rhythms within a dotted note context are far more irritating than for EM1, so it is appropriate to review and compare the differences between the systems that underlie EM1 and 2. that is the basis for all given meters. The differences between EM1 and EM2 are primarily notational, and everything said in the EM1 explanation still holds; however, the specifics of precisely locating embedded rhythms within a dotted note context are far more irritating than for EM1, so it is appropriate to review and compare the differences between the systems that underlie EM1 and 2.
Below are two charts (A & B) of subdivisions. They show, in musical notation, the subdivisions from 1 to 8 for five different note values. The five notes that are subdivided appear at the top, in row 1, one note per column. At the left of the chart are the subdivision fractions.
Chart (A) shows the subdivisions for non-dotted values.
Note that the successive 1:2 ratios of
hold; regardless of the superscript. |
Chart A
|
1 |
2 |
4 |
8 |
16 |
| 1 |
 |
 |
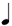 |
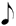 |
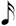 |
| 1/2 |
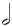 |
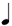 |
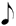 |
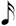 |
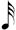 |
| 1/3 |
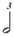 |
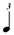 |
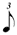 |
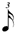 |
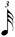 |
| 1/4 |
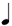 |
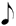 |
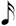 |
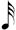 |
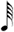 |
| 1/5 |
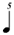 |
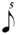 |
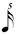 |
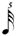 |
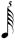 |
| 1/6 |
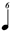 |
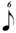 |
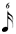 |
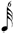 |
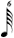 |
| * 1/7 |
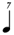 |
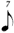 |
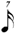 |
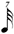 |
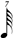 |
| 1/8 |
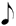 |
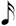 |
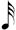 |
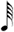 |
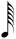 |
|
*This notation is the result of using the same unit between binary divisions.
It conflicts with Chart B below (row 1/7) and consequently certain composers (Carter especially) recommend halving the value for conformity (i.e. — the 1/7 line would read 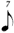 , , 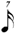 , , 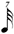 , , 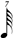 , , 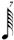 ). ). |
All notes in row 1 are my choices.
Dividing the values of row 1 by 1/2, 1/4, and 1/8 results in the usual given symbols that are found respectively on the rows labeled 1/2, 1/4, and 1/8.
The logic dictating what note value(s) to use between these geometric divisions is:
RULE 1: use the symbol for the larger value until the next rhythmic notation level has been reached, and the new symbol for that new level has been used.
This explains (as an example — for the 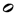 column) the use of the column) the use of the 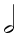 between 1/2 and 1/4; and the use of the between 1/2 and 1/4; and the use of the 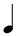 , between 1/4 and 1/8 until one reaches the , between 1/4 and 1/8 until one reaches the 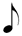 ; etc. However, in order to distinguish the intermediary divisions from the original value (for example, to distinguish between a regular ; etc. However, in order to distinguish the intermediary divisions from the original value (for example, to distinguish between a regular 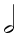 or a or a 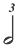 , one adds a superscript to indicate the actual arithmetic and durational value. , one adds a superscript to indicate the actual arithmetic and durational value.
There is some dispute regarding the notation for division by seven, i.e. whether, for example, one seventh of a 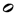 should be written as should be written as 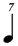 or or 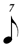 . On the grounds of both efficacy and internal consistency, certain composers (Carter especially) recommend the shorter-value alternative, and under those circumstances the 1/7 row of this chart would read: . On the grounds of both efficacy and internal consistency, certain composers (Carter especially) recommend the shorter-value alternative, and under those circumstances the 1/7 row of this chart would read:
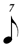 , , 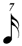 , , 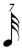 , , 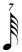 , , 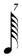 . .
The two most frequently proffered defenses for this shorter-value alternative are:
a) that 1/7 (= .143) of a beat is closer in duration to 1/8 (.125) than to 1/4 (.250), or in musical values (for a 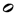 ) 1/7 is closer in speed to an ) 1/7 is closer in speed to an 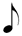 than to a than to a 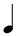 , and therefore the use of the smaller value serves as a mnemonic to move things along. The logic of this argument is inconsistent, as the same could be said for the sextuplet (.167), which is also closer in value to the , and therefore the use of the smaller value serves as a mnemonic to move things along. The logic of this argument is inconsistent, as the same could be said for the sextuplet (.167), which is also closer in value to the 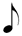 than to the than to the 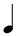 (for a visual aid, please see the "Chart of divisions in to 2 to 16 parts", lines 4 - 8) , but no one proposes that 1/6 of a (for a visual aid, please see the "Chart of divisions in to 2 to 16 parts", lines 4 - 8) , but no one proposes that 1/6 of a 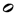 be notated using a be notated using a 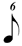 . .
b) as discussed briefly in a footnote to chart (B) below, there exists a minor inconsistency which may be minimized by notating non-dotted-rhythm septuplets using the smaller values.
Neither of these concerns have been sufficient to cause the majority of people to use the shorter-value alternative, so I have stayed with the more usual notation.
Let us now consider the relationships across each row.
The CRUCIAL point is:
RULE 2: that the geometric relations across and for each row ARE CONSERVED
either for
(a) rows without superscripts, or
(b) across values with the SAME superscripts or note suffixes (dots, double dots, etc). In other words, just as there are 2 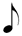 in 1 in 1 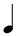 etc, there are ALWAYS 2 etc, there are ALWAYS 2 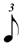 in 1 in 1 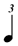 ; 2 ; 2 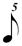 in 1 in 1 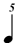 ; 2 ; 2 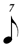 in 1 in 1 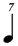 , etc. etc. , etc. etc.
In other words, the geometric ratios 1:2:4:8:16 etc remain inviolate, as long as all the note values are members of the same superscript i.e. all triplets, or all quintuplets, or septuplets etc.
This frequently overlooked fact is probably responsible for more miscalculation and misunderstanding of "complex" rhythmic notation than just about anything else.
Let us now turn to chart (B), which provides information similar to (A), but for dotted values.
Note that the successive 1:2 ratios of
hold; regardless of the superscript. |
Chart B
|
1 |
2 |
4 |
8 |
16 |
| 1 |
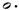 |
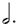 |
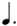 |
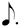 |
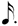 |
| 1/2 |
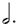 |
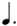 |
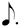 |
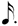 |
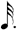 |
| 1/3 |
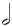 |
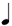 |
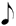 |
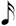 |
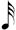 |
| 1/4 |
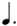 |
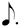 |
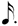 |
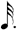 |
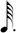 |
| 1/5 |
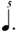 |
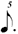 |
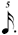 |
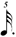 |
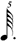 |
| 1/6 |
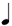 |
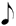 |
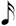 |
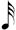 |
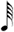 |
| ** 1/7 |
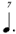 |
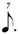 |
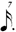 |
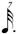 |
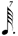 |
| 1/8 |
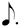 |
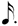 |
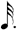 |
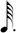 |
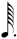 |
|
**This notation is the result of a process of elimination. One seventh of 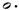 cannot be cannot be 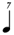 because this is identical to 1/7 of a normal whole-note. It cannot be because this is identical to 1/7 of a normal whole-note. It cannot be 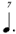 because we have already used a shorter value ( because we have already used a shorter value ( 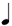 being in use at 1/6). Therefore, being in use at 1/6). Therefore, 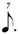 remains — causing the discrepancy mentioned above. remains — causing the discrepancy mentioned above. |
As before, row 1 are my choices. The symbols for rows 1/2, 1/4, and 1/8 are those of chart (A), but with the addition of a dot next to all notes, so as to be consistent with the dot that has been added to the whole note.
This addition of the dot across values may appear to be merely a convention, but is not.
By definition a 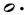 = 6 = 6 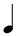
1/2 of 6 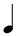 = 3 = 3 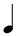 = 1 = 1 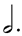 . .
One can perform similar calculations for both 12 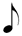 and 24 and 24 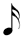 , (both of which = 1 , (both of which = 1 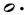 ), resulting in the symbols found respectively in rows 1/4 and 1/8 of col. 1. ), resulting in the symbols found respectively in rows 1/4 and 1/8 of col. 1.
One can also derive the values for 1/3 and 1/6: i.e.
1/3 of a 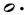 = 2 = 2 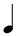 = 1 = 1 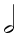 , ,
1/6 of a 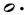 = 2 = 2 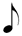 = 1 = 1 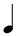 . .
This leaves remaining the rows marked 1/5 and 1/7th.
In regards 1/5, as this value occurs between 1/4 and 1/6, whose musical symbols are already given, one uses the symbol for the longer value and adds the number 5 as a superscript — in the specific case of the 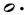 that means a that means a 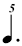 . .
An additional reason for using the 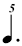 is that if one just used a is that if one just used a 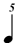 (i.e. without a dot) that would be exactly the same notation as used in chart (A), and the entire point of this exercise is to distinguish the values within chart (B) from those of chart (A), so that the underlying meters will be more apparent. (i.e. without a dot) that would be exactly the same notation as used in chart (A), and the entire point of this exercise is to distinguish the values within chart (B) from those of chart (A), so that the underlying meters will be more apparent.
In regards 1/7, the use of 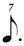 is the result of a process of elimination. One seventh of a is the result of a process of elimination. One seventh of a 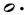 cannot be a cannot be a  as that is already employed for 1/7 of a as that is already employed for 1/7 of a 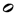 (see in chart (A)). One seventh of a (see in chart (A)). One seventh of a 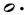 also cannot be a also cannot be a 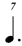 as the progression of the duration-symbols within chart (B) would then be non-monotonic, given that we would have already used a shorter value (the as the progression of the duration-symbols within chart (B) would then be non-monotonic, given that we would have already used a shorter value (the 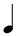 being used for 1/6). Therefore, being used for 1/6). Therefore, 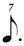 remains — causing the discrepancy with chart (A) that is mentioned above, i.e. in chart (A) 1/7 is notated in remains — causing the discrepancy with chart (A) that is mentioned above, i.e. in chart (A) 1/7 is notated in 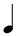 (and not in (and not in 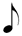 ) unless (for chart A) one switches to the alternative notation for septuplets. ) unless (for chart A) one switches to the alternative notation for septuplets.
As regards the EM2 itself, meters appear on the left, descending the page, and the 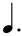 is the basis for all meters used. The numbers across the top of the matrix are the number of embedded divisions for that column. If the number of divisions in a column = the number of beats of a meter, the notes within the cell which exists at the intersection of that row and that column are in the lightest possible shade of grey. If one wants to change the denominator of a meter, one should add or remove a set of beams, just as with EM1. is the basis for all meters used. The numbers across the top of the matrix are the number of embedded divisions for that column. If the number of divisions in a column = the number of beats of a meter, the notes within the cell which exists at the intersection of that row and that column are in the lightest possible shade of grey. If one wants to change the denominator of a meter, one should add or remove a set of beams, just as with EM1.
As with EM1, in order to find the exact placement-pattern for a specific X:Y ("X in the space of Y"), find the row labeled X , and the column labeled Y, and locate the cell which exists at the intersection of that row and column. The method(s) of practicing remain the same. Indeed, unless the tempo is slow, and the 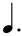 are being subdivided into are being subdivided into 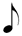 , there is no fundamental difference in the performance of, for example, 5:3 , there is no fundamental difference in the performance of, for example, 5:3 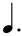 or 5:3 or 5:3 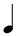 — we are speaking only of a notational convention, and not a task to be solved "de novo" (CAVEAT: see later for problems that can arise when the tempo IS slow!). If you refer to the explanation of EM1 (see the last 7 paragraphs directly before the footnotes) where, with no trouble at all, we found 32 ways to write "FIVE" in the space of something, here are at least another 21 per column (if we alter the denominator of the time signature), with no fundamental change. These are all "FIVE" and partake equally of "five-ness", no matter how outré the notation. — we are speaking only of a notational convention, and not a task to be solved "de novo" (CAVEAT: see later for problems that can arise when the tempo IS slow!). If you refer to the explanation of EM1 (see the last 7 paragraphs directly before the footnotes) where, with no trouble at all, we found 32 ways to write "FIVE" in the space of something, here are at least another 21 per column (if we alter the denominator of the time signature), with no fundamental change. These are all "FIVE" and partake equally of "five-ness", no matter how outré the notation.
The RULE for finding other exemplars remains the same, except that one must be comfortable with the subdivisions for dotted values found in chart (B) above, and one must be aware that, when calculating a pattern that does not exist in EM2, (or proofing a pattern which does!) the choice of an appropriate B (in using the formula X:YB) is particularly important. To pursue this, consider 5:21 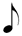 (as an arbitrary example). There will be composers who may prefer to notate this time signature as 5:7 (as an arbitrary example). There will be composers who may prefer to notate this time signature as 5:7 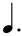 which one would think is much the same thing as 5:21 which one would think is much the same thing as 5:21 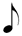 , but will result in an entirely different notation of the embedded pattern. For 5:21 , but will result in an entirely different notation of the embedded pattern. For 5:21 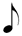 the rule for rewriting asks us to divide each B (the the rule for rewriting asks us to divide each B (the 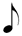 ) into 5 parts ( ) into 5 parts ( 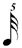 ) and then take 21 of them at a time, resulting in the pattern that may be found within EM2 — (also see ex. (a) 5:21 below). For 5:7 ) and then take 21 of them at a time, resulting in the pattern that may be found within EM2 — (also see ex. (a) 5:21 below). For 5:7 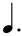 we still divide each B into 5 parts, but dividing a we still divide each B into 5 parts, but dividing a 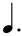 into 5 parts results in units of into 5 parts results in units of 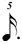 , which we then take 7 at a time, resulting in the pattern of ex. (b) 5:7 below. , which we then take 7 at a time, resulting in the pattern of ex. (b) 5:7 below.
| (a) 5:21 |
|
(b) 5:7 |
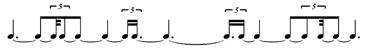 |
|
 |
Both patterns are arithmetically correct, and are congruent with each other, but provide different metrical information, and which pattern is more appropriate and/or efficacious depends on various factors. As an example of one of these factors — at a slow tempo, with the 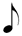 s being beaten, the pattern 5:7 s being beaten, the pattern 5:7 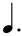 will not provide the information needed to easily place the attacks relative to the beaten or thought will not provide the information needed to easily place the attacks relative to the beaten or thought 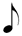 ; whereas at a quick tempo, 5:21 ; whereas at a quick tempo, 5:21 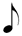 will provide excess detail that is probably counterproductive. will provide excess detail that is probably counterproductive.
The discussion of EM1 regarding handedness and the psychology of production remains valid and applicable, as do the instructions regarding performance. Indeed, if you are comfortable with all the elements of EM1, you need only recognize the dotted notation of EM2 for the phantasmagoria it is.
Paul Zukofsky
March 2004
|