Matrix of Embedded Rhythms
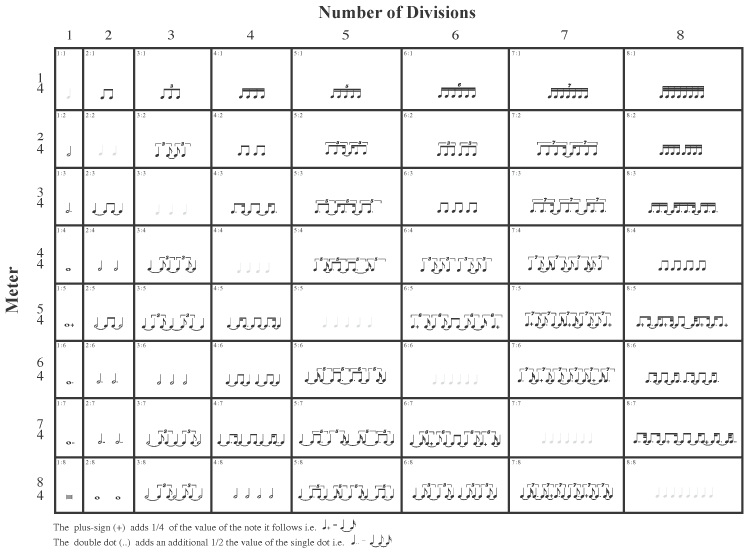
Click on image to see a larger version of the chart
Matrix of Embedded RhythmsClick on image to see a larger version of the chart |
|
Among the most frequent requirements of newer rhythmic practice is the task to perform some number of attacks within the space of some different number of beats, the attacks and beats not being related to each other in the usual binary fashion i.e.  The most familiar of this type of task are triplets, as in  which is spoken of as " three triplet-quarter-notes in the space of two regular quarter-notes" (we will later omit the word "regular", but for now we must fix in our minds that these are two very different species of quarter notes!). But even for these familiars we do not always know the exact placement of the individual attacks (other than for the coincident beat — which is usually the downbeat). The above matrix provides patterns for the exact placement for 64 varieties of what I refer to as embedded or combination rhythms. These are also more commonly called composite rhythms, but I firmly believe that term is far better reserved for the more general problem of the totality of all rhythmic attacks that occur within a given musical context. The matrix should be read as follows: On the left side, descending the page, are meters. Each meter applies for that entire row of the matrix. The Across the top of the matrix are the number of divisions within a column. These divisions represent the embedded meter or value, except (of course) in those cases where the number of divisions in a column equals the number of beats of a meter. In these cases, the notes are in the lightest possible shade of grey, so as to differentiate. As an example, in order to find the exact placement for 3:2 The answer is: If, on the other hand, one wanted the composite for 2:3  There are many ways to practice these rhythms. The simplest is to mentally remove the ties of the notated values, and sing or tap the result of combining the embedded (columnar) value with the required meter. For example, if one were to be studying 4:3 (4 in the space of 3), one would tap:  Another way of studying would be to count or tap out all the internal subdivisions, emphasizing those points that coincide with the embedded values. For example, if one were studying 4:5
one234 2two34 32three4 423four 5234 or more easily one234 1two34 12three4 123four 1234 where, in
i.e.  whereas if one were studying 5:4 one234five 223four5 32three45 4two345 or more easily one234five 123four5 12three45 1two345 or in rhythmic notation  Another way of studying these rhythms is to have one hand tap the embedded portion, and the other hand tap the required meter. For example, if one were to be studying 5:3, the hand distribution might be: 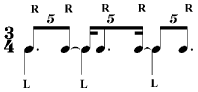 When practicing, note that it is also invaluable to reverse the hand distribution. Having the embedded portion in the right hand with the required meter in the left is not the same problem as the reverse, nor is it the same as reversing the metric ratio. As explanation, consider the 2 X 2 matrix below: 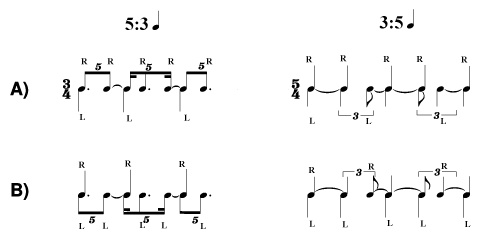 Clearly the patterns in the 5:3 column are identical save for the fact that the hand-tasks are reversed, but note that this physiological reversal is not immediately automatic, or "simple"; i.e. for many, it feels a somewhat different problem. Similarly, the patterns in the 3:5 column are also identical except for the handedness, but again the switch is not always autonomic (in the motor-skills sense of the word).1 In regards the rows, upon consideration it is clear that the patterns of row A are arithmetically and physiologically equivalent, but they are far from psychologically equivalent. Furthermore, if we assume that the One need not reserve a special time to practice these patterns. As long as they are memorized, they can be practiced as you are walking, counting the embedded portion against your paces, or if sitting on a bus or subway, you can tap them using one finger from each hand. Indeed, it may prove advantageous to practice these patterns in a public space, for if you do so with supreme concentration, combined with a Harpo-Marx-like Gookie, you may find yourself with far fewer people surrounding you than otherwise might have been the case. These rhythms may also be distributed between two persons, or even two groups of people — i.e. in the case of X:Y one person would attempt to count and perform the X against the Y of the other person. The participants should then reverse roles. It is advantageous to not only practice these patterns one by one, but to also practice them in chains, one immediately following the other without pause. For example, one might take a single row (meter) and create a succession of patterns that follow each other (as might happen in an actually composition), and one should do this (in principle) for each row. Similarly one could concentrate on a single column, varying the meter for each new pattern. Ultimately one should create arbitrary successions of patterns across rows and columns. For all of these practice situations, it is probably wise to at first repeat each pattern an agreed-upon number of times before switching (without pause) to another pattern, but the goal is to switch patterns each "bar". All of these rhythms are self-retrogradable. In other words, each rhythm reads the same backwards as forwards. If you copy out these rhythms, or ever need to create a version of a similar rhythm which is not on the chart, and the result is not exactly symmetrical and self-reversible, you have made an error in your calculations or copying. All of these types of rhythms follow a simple arithmetic rule, which may be used to create exemplars not found on the chart: for any rhythm X:YB (read as X in the space of Y Beats), where X always represents the number to the left of the ratio (:) sign RULE1) first divide B into X parts — this provides the smallest subdivision one needs to count. 2) take the result of Step 1) and count-off Y subdivisions, repeating this process until all the subdivisions of 1) are finished — this process will provide the exact placement of the attack points for the embedded rhythm. Note that there will always be X groups of these Y subdivisions. 3) After completing Step 2) be certain (by using multiples of Y, or if those multiples go past a beat, by using ties) to rewrite the results of Step 2) in terms of B. As a simple example of this procedure, consider 4:3 In this case X (the number to the left of the ratio (:) sign) = 4 Step 1) above tells us to divide B (in this case a Step 2) above tells us to take the result of Step 1) (in this case a  Now we know that When you have worked through this process, and have rewritten the results of Step 2) so as to conform to the underlying meter, the final result is:  Now there are those who propound a common denominator approach to solving these problems. As an example, in the aforesaid problem of 4:3 The problem with this approach is that it does not answer the two questions: a) 12 what?
To continue the argument, consider 4:3 Another way of saying this is that 4:3 In short, the common denominator solution is not a good one, as it does not provide enough information (i.e. what type of note value should one be thinking). Finally, there is the matter of performing these types of rhythms. It is true that, for all of these types of patterns, one must begin the learning process by attempting to have the attacks as arithmetically correct as possible. However, arithmetic exactitude is only a means to an end. It is not, and cannot be, the end itself. Arithmetic exactitude will not provide the shaping necessary to convey the sentiment of a waltz, let alone a waltz embedded in a What are the practical implications of these assertions? For the sake of argument, consider that cell within the matrix which exists at the intersection of column 5, and the row marked 
Count (preferably out loud — but it will also work silently) these five Now observe every cell in the column marked 5. Each cell in that column has five attacks, just as does the Hence the reason composers so often take refuge in simply notating five equal values of some sort within a bracket over the space demanded, and if the performer is lucky, the composer will specify the "in the space of" dividend, leaving to us the nitty-gritty of determining the quotient. While this enormous dichotomy between the underlying unity of the patterns (they all possess and partake of "five-ness"), and the epidemic of notational possibilities, is endemic to our system of rhythmic notation, there is a distortive aspect whose virulence we cannot, must not, minimize. Remember the architectural adage: form follows function. Applied here, it implies that the form of the notation must follow the need (the function) to convey a group of five. It is the five that contains the "quality" we have remarked upon and which is the important factor, not the notational garb it must assume so that we can accurately do our job. In addition, just as the column of five has the quality of "five-ness", so does every other column have its own quality (or should) — and it is those qualities, no matter how horrifying the precise notation, that are of paramount importance. None of the above means that one has license to distort beyond recognition. What it does imply is that one begins by doing as well as one can, and trains to be as accurate as is humanly possible, and part of that training is knowing these rewritten patterns, and more importantly, how to rewrite them — but thereafter, after you have tried to understand why the composer is using such rhythms, and after you have given thought to what you think needs to be aurally conveyed, so that the underlying purpose and structure of the idea is clarified, and especially after the trajectory of the embedded pattern is "in your blood", then shape the pattern — very slightly — so as to better convey its intrinsic meaning and motivation. Paul Zukofsky Footnotes
|
is the basis for all given meters. If one wants to employ the patterns for 
meters, add an additional set of beams to the notation within the cells of the matrix. For 
meters, for each cell, remove a set of beams, or if no beams, multiply the note values by two.
, and the column labeled 
, and the column labeled 
one might speak:
, one has the repetition of the 5 beats of
each, with emphasis on the 4 embedded accents
of the 5:3 column = the 
of right 3:5 column, the patterns of row 
, the smallest subdivision needed.
and then count-off groups of 
so to the greatest extent possible we should write the rhythm using 
BUT WE CANNOT exclusively use these values AS WE WISH TO SHOW AND KNOW WHERE THE BEAT IS.
, whereas 3:4 
.
context. Arithmetic exactitude will not allow one to shape an embedded rhythm so that one can maintain the same trajectory of phrase across different tempi which happen to be written out using so-called irrational rhythms (i.e. think Babbitt). Arithmetic exactitude in-and-of-itself as a goal will rarely convey any meaning, other than an attempt at exactness.
, in other words
cell. It is sometimes horrendously difficult to realize that, looking up and down all cells in the column, especially when you look at 
, 
and 
, but nevertheless, there are five attacks per cell. Indeed, if one were to perform the proper metric modulations, there is no reason why all these differently notated avatars of five attacks could not be performed at exactly the same speed. That the five attacks in each cell have not been vertically uniformly aligned is due not only to the restrictions of the typesetting program, but also to the fact that visually we would reject the image, and/or fail to comprehend how many beats it fills. Furthermore, this column shows only eight different ways in which to write "